Programming a simple minimax chess engine in R

Improving our chess logic: heuristic position evaluation function

While playing a full random game is surprisingly simple with the help of the rchess package, we would like to start improving our engine in two ways:

• Evaluation function: implement a simple heuristic to evaluate individual positions based on the pieces on the board and the safety of the king
• Search function: implement an algorithm that allows our engine to search through positions multiple moves ahead

Let’s first work on the position evaluation function, which is usually performed from the perspective of white. More precisely, scores greater than zero indicate an advantage for white and scores less than zero point to an advantage for black. Our scores are based on three aspects of the position being evaluated:

• Is this position a win for one of the players or a draw? If white won the score is 1000. If black won the score is -1000. In case of a draw the score in 0.
• What is the material advantage for white? Each piece receives a value (9 points for queens, 5 points for rooks, 3 points for bishops and knights and 1 point for pawns) and the total piece value for black is subtracted from the total piece value for white.
• If the white king is in check subtract one point from the position score. If the black king is in check add one point to the position score.

This is a fairly standard (although highly simplified) way to define an evaluation function: white will choose moves with high scores and black will prefer moves with low scores. Both players can thus use the same position evaluation function, which simplifies our program.

Let’s implement these simple heuristics in R:

# Position evaluation function
evaluate_position <- function(position) {
  # Test if black won
  if (position$in_checkmate() & (position$turn() == "w")) {
    return(-1000)
  }
  # Test if white won
  if (position$in_checkmate() & (position$turn() == "b")) {
    return(1000)
  }
  # Test if game ended in a draw
  if (position$game_over()) {
    return(0)
  }

  # Compute material advantage
  position_fen <- strsplit(strsplit(position$fen(), split = " ")[[1]][1], split = "")[[1]]
  white_score <- length(which(position_fen == "Q")) * 9 + length(which(position_fen == "R")) * 5 + length(which(position_fen == "B")) * 3 + length(which(position_fen == "N")) * 3 + length(which(position_fen == "P"))
  black_score <- length(which(position_fen == "q")) * 9 + length(which(position_fen == "r")) * 5 + length(which(position_fen == "b")) * 3 + length(which(position_fen == "n")) * 3 + length(which(position_fen == "p"))

  # Evaluate king safety
  check_score <- 0
  if (position$in_check() & (position$turn() == "w")) check_score <- -1
  if (position$in_check() & (position$turn() == "b")) check_score <- 1

  # Return final position score
  return(white_score - black_score + check_score)
}

Applying this function to our previous game we see that it correctly recognizes a win by white by returning a score of 1000:

evaluate_position(chess_game)

## [1] 1000

Improving our chess logic: minimax search

So far we have implemented a function that quantifies whether a given position is advantageous for white or black. The second part of our engine builds on this result and focuses on searching through potential next moves to identify the best choice. We will use an algorithm called minimax to perform this search.

The figure below shows how minimax works on a toy example:

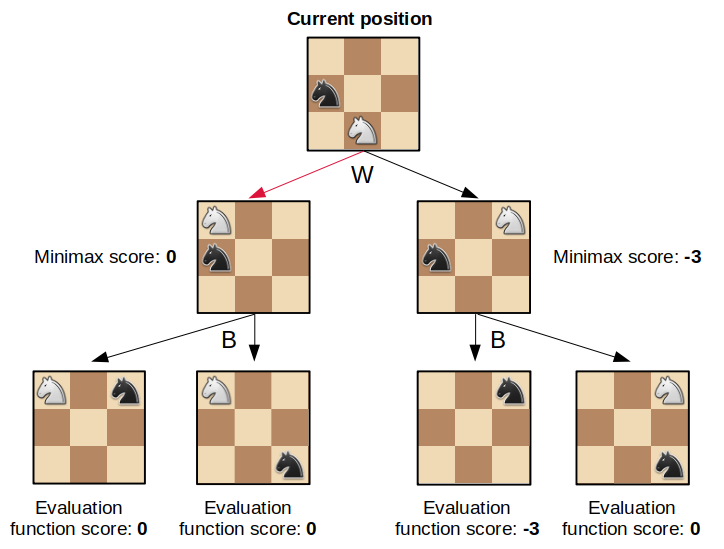
Figure 1: Example of minimax search for the best next move (white to move in the current position)

White starts at the root position and has two move options. For each option, black has two replies available. Figure 1 summarizes this tree of move possibilities and shows the heuristic score for each of the leaf nodes based on the position evaluation function we just defined.

Black will always pick the move that minimizes the heuristic score. In the right branch black will play the move that results in a score of -3, so white can predict that picking the right branch move will lead to a position with score -3. Picking the left branch move however will result in a score of 0, since black cannot capture any material. Based on this reasoning, white will chose the left branch since it leads to a more advantageous outcome even after black plays its best reply.

This minimax strategy is powerful in chess since it looks multiple moves ahead and evaluates positions assuming that each player makes optimal choices. We can also increase the height of this tree: the position evaluation will be more precise since more moves are tested but the runtime will also increase.

Let’s implement this algorithm in R:

# Score position via minimax strategy
minimax_scoring <- function(chess_game, depth) {
  # If the game is already over or the depth limit is reached
  # then return the heuristic evaluation of the position
  if (depth == 0 | chess_game$game_over()) {
    return(evaluate_position(chess_game))
  }

  # Run the minimax scoring recursively on every legal next move, making sure the search depth is not exceeded
  next_moves <- chess_game$moves()
  next_move_scores <- vector(length = length(next_moves))
  for (i in 1:length(next_moves)) {
    chess_game$move(next_moves[i])
    next_move_scores[i] <- minimax_scoring(chess_game, depth - 1)
    chess_game$undo()
  }

  # White will select the move that maximizes the position score
  # Black will select the move that minimizes the position score
  if (chess_game$turn() == "w") {
    return(max(next_move_scores))
  } else {
    return(min(next_move_scores))
  }
}

This completes the minimax_scoring function that returns a score given an input position. Now we just need a wrapper function to evaluate all legal next moves via minimax_scoring and return the optimal choice:

# Select the next move based on the minimax scoring
get_minimax_move <- function(chess_game) {
  # Score all next moves via minimax
  next_moves <- chess_game$moves()
  next_move_scores <- vector(length = length(next_moves))
  for (i in 1:length(next_moves)) {
    chess_game$move(next_moves[i])
    # To ensure fast execution of the minimax function we select a depth of 1
    # This depth can be increased to enable stronger play at the expense of longer runtime
    next_move_scores[i] <- minimax_scoring(chess_game, 1)
    chess_game$undo()
  }

  # For white return the move with maximum score
  # For black return the move with minimum score
  # If the optimal score is achieved by multiple moves, select one at random
  # This random selection from the optimal moves adds some variability to the play
  if (chess_game$turn() == "w") {
    return(sample(next_moves[which(next_move_scores == max(next_move_scores))], size = 1))
  } else {
    return(sample(next_moves[which(next_move_scores == min(next_move_scores))], size = 1))
  }
}

The function get_minimax_move defines the complete logic for our computer chess player. We are now ready to test the performance of our algorithm.

Testing our R minimax chess engine

Let’s first test the performance of our minimax-based chess engine by letting it play 10 games as white and 10 games as black against the random move generator we defined at the beginning of this article. If everything works as expected then our engine should win every time:

# Function that takes a side as input ("w" or "b") and plays 10 games
# The selected side will choose moves based on the minimax algorithm
# The opponent will use the random move generator
play_10_games <- function(minimax_player) {
  game_results <- vector(length = 10)
  for (i in 1:10) {
    chess_game <- Chess$new()
    while (!chess_game$game_over()) {
      if (chess_game$turn() == minimax_player) {
        # Selected player uses the minimax strategy
        chess_game$move(get_minimax_move(chess_game))
      } else {
        # Opponent uses the random move generator
        chess_game$move(get_random_move(chess_game))
      }
    }
    # Record the result of the current finished game
    # If mate: the losing player is recorded
    # If draw: record a 0
    if (chess_game$in_checkmate()) {
      game_results[i] <- chess_game$turn()
    } else {
      game_results[i] <- "0"
    }
  }

  # Print the outcome of the 10 games
  print(table(game_results))
}

White wins every game by playing the minimax strategy against the random move generator:

play_10_games("w")

## game_results
##  b 
## 10

Black also wins every game as the minimax player against random white moves:

play_10_games("b")

## game_results
##  w 
## 10

This simple experiment shows that our minimax chess engine is indeed more powerful than a random move generator, but this is a fairly low bar. I have also tested this program against multiple chess apps and it was able to win games against opponents playing at a casual difficulty level. Increasing the minimax depth leads to stronger play, but evaluating more than four moves in advance was not feasible on my computer due to long runtimes.

Conclusion and next steps

Overall this simple R chess engine is fun to play against for a beginner or casual player, and writing it was a great way to practice the minimax algorithm. Numerous improvements can still be made.

Some updates that I plan to discuss in future posts are:

• Implement alpha-beta pruning to decrease the number of positions evaluated by minimax.
• Use negamax to further simplify the code.
• Leverage neural networks to define a better position evaluation function. The tensorflow and keras R packages make it possible to build very flexible neural networks within R.

Programming a simple chess engine is an exciting journey through the many machine learning capabilities offered by R. Looking forward to the next steps!

For a full collection of R programming tutorials and exercises visit my website at codeRtime.org and the codeRtime YouTube channel.